Voids in Solid

As we have learn earlier the max packing faction is 74% (in HCP Or FCC) and the remaining space is void. Voids in solids is the vacant space between the constituent particles in a closed packed structure.
The size and distribution of voids in solid have a considerable effect on behaviour of materials property. eg, More is the void more will be diffusivity, and also affect the interstitial solubility.

Types of Voids :
    (1) Tetrahedral
    (2) Octahedral

Tetrahedral Void :
The tetrahedral Void form in crystal structure when the sphere of top layer lie just above the triangular voids formed be layer lying just below. A tetrahedron is formed by joining radius of all four spheres and the vacant space between them is tetrahedral void.

Octahedral Void :
The Octahedral Void form in crystal structure is between a triangular voids of first layer coincides ( having different orientation ) with the triangular voids of layer above or below it. A octahedron is formed by joining radius of all four spheres and the vacant space between them is octahedral void.

Voids in FCC

Tetrahedral Void in FCC :

➧ The FCC crystal structure have 8 tetrahedral voids which are located near the corners of cell. All Tetrahedral voids lie inside the cell
➧ The number of tetrahedral voids is 2 times the number of the atoms in cell.
➧ The size of largest interstitial atom that can fit into tetrahedral Void = \( 0.225 \times \textrm{ Size of FCC atoms} \) \[ \textrm{n atoms} \Rightarrow 2 \times \textrm{n Tetrahedral Void} \]

Octahedral Void in FCC :

➧ The FCC crystal structure have 4 octahedral voids which are located at the :
      1) Center of cell = 1
      2) At every edge center contributing 1/4th => \( \frac{1}{4} \times 12 = 3 \) Voids
➧ The number of octahedral voids is equal to the number of the atoms in cell.
➧ The size of largest interstitial atom that can fit into octahedral Void = \( 0.414 \times \textrm{ Size of FCC atoms} \) \[ \textrm{n atoms} \Rightarrow \textrm{n Octahedral Void} \]

Voids in BCC

➧ The BCC materials have distorted Tetrahedral and Octahedral voids.
➧ Number of Tetrahedral voids : 12
➧ Number of Octahedral voids : 6

Voids in HCP

➧ Number of Total Tetrahedral voids : 12 or 4 Voids/cell
➧ Number of Total Octahedral voids : 6 or 2 Voids/cell

---

Crystal	Void	Position	\( \frac{voids}{unit} \)	\( \frac{voids}{atoms} \)	\( \frac{r_{voids}}{r_{atoms}} \)
FCC	Tetrahedral	8 \( ( \frac{1}{4}, \frac{1}{4}, \frac{1}{4} ) \)	8	2	0.225
	Octahedral	Body Center : 1 \( ( \frac{1}{2}, \frac{1}{2}, \frac{1}{2} ) \) Edge Center : 3 \( ( \frac{1}{2}, 0, 0 ) \)	4	1	0.414
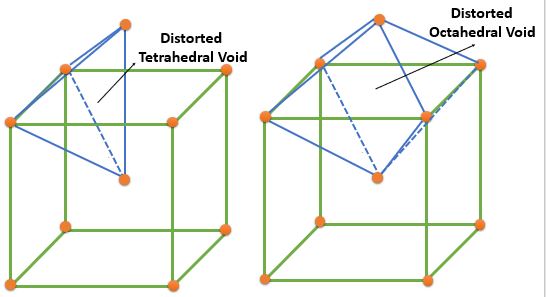
BCC	Distorted Tetrahedral	\( \frac{4}{2} \times 6 = 12 ( 0, \frac{1}{2}, \frac{1}{4} ) \)	12	6	0.155
	Distorted Octahedral	Face Center : \( \frac{1}{2} \times 6 = 3 ( \frac{1}{2}, \frac{1}{2}, 0 ) \) Edge Center : \( \frac{1}{4} \times 12 = 3 \( ( \frac{1}{2}, 0, 0 ) \)	6	3	0.291
HCP	Tetrahedral	\( ( 0, 0, \frac{3}{8} ) , ( 0, 0, \frac{5}{8} ) \) \( ( \frac{2}{3}, \frac{1}{3}, \frac{1}{8} ) , ( \frac{2}{3}, \frac{1}{3}, \frac{7}{8} ) \)	4	2	-
	Octahedral	\( ( \frac{1}{3}, \frac{2}{3}, \frac{1}{4} ), ( \frac{1}{3}, \frac{2}{3}, \frac{3}{4} ) \)	2	1	-