Miller Indices

Miller Indices (hkl), is the set of number which indicates the orientation of plane or set of parallel planes of atoms in a crystal. It is calculated by taking reciprocals of fractional intercepts taken along the three crystallographic direction and it is written inside parenthesis withous comma.
Miller indices notations :
(hkl) => Plane
{hkl} => Family of Planes
[hkl] => Direction
<hkl> => Family of direction

Steps to calculate miller indices :

Example 1:

Steps	X	Y	Z
Intercept	\[ 1 \]	\[ 1 \]	\[ \infty \]
Reciprocal	\[ 1 \]	\[ 1 \]	\[ 0 \]
Rationalise	\[ 1 \]	\[ 1 \]	\[ 0 \]
Miler Indices	\[ (1 1 0) \]

Example 2:

Steps	X	Y	Z
Intercept	\[ 1 \]	\[ 1 \]	\[ \frac{1}{2} \]
Reciprocal	\[ 1 \]	\[ 1 \]	\[ 2 \]
Rationalise	\[ 1 \]	\[ 1 \]	\[ 2 \]
Miler Indices	\[ (1 1 2) \]

Example 3:

Here the axis is not passing through the intercept. In such cases we have to shift the origin. Miller Indices 210

Steps	X	Y	Z
Intercept	\[ \frac{1}{2} \]	\[ 1 \]	\[ \infty \]
Reciprocal	\[ 2 \]	\[ 1 \]	\[ 0 \]
Rationalise	\[ 2 \]	\[ 1 \]	\[ 0 \]
Miler Indices	\[ (2 1 0) \]

Question :Find the miller indices of given vector in below figure
Miller Indices -211

Show Answer

Answer : [-2 2 1]

Here all the axis is not passing through the intercept. In such cases we have to shift the origin.

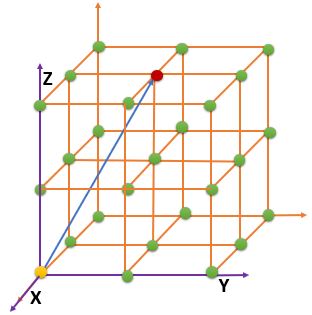
Steps	X	Y	Z
Intercept	\[ -1 \]	\[ 1 \]	\[ 2 \]
Reciprocal	\[ -1 \]	\[ 1 \]	\[ \frac{1}{2} \]
Rationalise	\[ -2 \]	\[ 2 \]	\[ 1 \]
Miler Indices	\[ [-2 2 1] \]

Properties of Miller Indices :

Plane which are close to origin have higher miller indices than plane which are far away from origin
If a plane is parallel to any axis then its corresponding miller index on that axis wll be zero
Two parallel planes will have same Miller Indices . Note :- Sign may change depending on there position.
Angle between two planes having miller indices \( ( h_{1} k_{1} l_{1}) \) and \( ( h_{2} k_{2} l_{2}) \) will be - \[ cos (\theta) = \frac{ h_{1}h_{2} + k_{1}k_{2} + l_{1}l_{2}}{ \sqrt{h_{1}^2 + k_{1}^2 + l_{1}^2} \times \sqrt{h_{2}^2 + k_{2}^2 + l_{2}^2} } \]
Two planes having miller indices \( ( h_{1} k_{1} l_{1}) \) and \( ( h_{2} k_{2} l_{2}) \) will be perpendicular to each other when - \[ h_{1}h_{2} + k_{1}k_{2} + l_{1}l_{2} = 0 \]

Interplaner Spacing (d)

Interplanar spacing is the separation between sets of parallel planes formed by the individual atoms in the lattice structure considering one plane passing through origin. \[ d = \frac{a}{\sqrt{h^2 + k^2 + l^2}} \] Where a = Lattice parameter

Question :The inter-planar spacing between the (2 2 1) planes of a cubic lattice of edge length 900 nm is: __________ nm
Show Answer

Answer : d = 300nm
As given a = 900nm
And Miller indices of plane is (2 2 1)
=> \( d = \frac{900}{\sqrt{2^2 + 2^2 + 1^2}} nm \)
=> \( d = \frac{900}{ 3 } \)
=> \( d = 300nm \)

Miller Indices for HCP

For HCP, the miller indices are denoted as (uvtw) for planes and [uvtw] for direction.
Note: Here t = - (u + v) HCP

Basal Plane & direction: \( (0 0 0 1)[1 1 \bar{2} 0] \)

Prismatic Plane & direction: \( (1 0 \bar{1} 0)[1 1 \bar{2} 0] \)

Basal Plane & direction: \( (\bar{1} 0 1 1)[1 1 \bar{2} 0] \)

Learn Metallurgy

Miller Indices

Properties of Miller Indices :

Interplaner Spacing (d)

Miller Indices for HCP

BLOGS

Learn Metallurgy

Links

Location