Deformation by Slip

Slip :
Sliding of blocks of the crystal over one another along a defined crystallographic plane known as Slip. It causes plastic deformation in metals. Slip System : The combination of slip plane and slip direction.
Slip Plane : Plane on which easiest slippage occures, which is the plane with highest planer density.
Slip direction : Direction on which easiest movement of dislocation possible i.e., Diretion having highest linear density.

Crystal	Metals	Slip Plane	Slip Direction	Number of Slip System
FCC	Cu, Al, Ni, Ag, Au	{111}	<110>	12
BCC	α-Fe, W, Mo	{110}	<111>	12
	α-Fe, W	{211}	<111>	12
	α-Fe, K	{321}	<111>	24
HCP	Cd, Zn, Mg, Ti, Be	{0001}	\( <11\bar{2}0> \)	3
	Ti, Mg, Zr	{\( {10\bar{1}0} \)}	\( <11\bar{2}0> \)	3
	Ti, Mg	{\( {10\bar{1}1} \)}	\( <11\bar{2}0> \)	6

Theoretical Shear Stress for Slip

• The above image show a SIMULTANEOUS BOND BREAKING MODEL.
• Means slip occures by breaking of all bonds simultaneously on imposing shear stress.
• As the slip occure by translation of one plane over another, and for this movement to occure in a perfect crystal a shere stress (\( \tau \)) is required.
• The distance betwwen atoms in the slip direction is b, and the spacing between adjecent lattice plan is a.

From the plot below we can easily conclude that -
    • The shear stress is initially zero when the two plans are in concidence. and it is zero when moved distance is multiple of b.
    • The shear stress is also zero when the atoms of top plane are midways between those of bottome plane.
    • And to break the bonds, the applied stress required to overcome the lattice resistance to shear is indicated by \( \tau_{max} \).
From Above fig. the first approximation of realtionship between shear stress and displacement can be expressed by sine function as - \[ \tau = \tau_{max} \big(sin \frac{2\pi x}{b} \big) \] For maimum shear stress x=a, and for small value of a/b the above equation can be written as - \[ \tau = \tau_{max} \Big(\frac{2\pi a}{b} \Big) \] As for rough approximation b = a, and also as \( \tau = G\gamma \) \[ \boxed{ \Rightarrow \tau_{max} = \frac{G}{2\pi} } \] Where \( \tau_{max} \) = Theoratical shear strength, and G = Shear Modulus.

Note : The observed shear strength is about 100 times smaller than the Theoratical shear strength. Which indicates that some other mechanism might be responsible for slip. In next section we are going to study such mechanism.

Slip by Dislocation movement

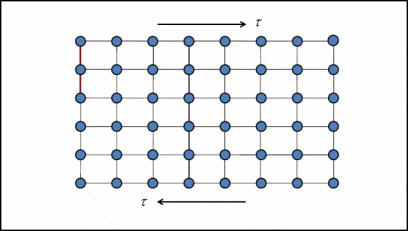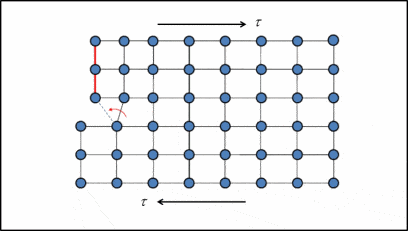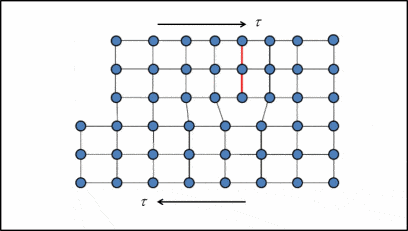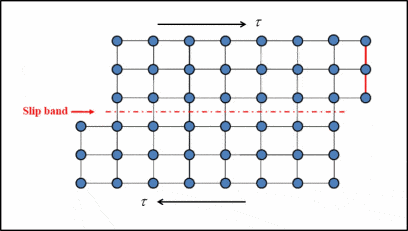
• The movement of dislocation is related with the Caterpillar Movement
• In this model we only move planes bit by bit instead of whole plane at once. which reduces the shear stress required to slip.
• This model was introduced by peierls nabarro and the steess predicted by this model is called as peierls nabarro stress or lattice friction.
• He also introduce a fact that dislocation has a width. The width of the dislocation is the distance on either side of dislocation upto with dislocation stess is applicable.
• Narrow dislocation are difficult to move.
\[ \boxed{ \tau_{PN} = \frac{2G}{1-\nu} exp{\Big(- \frac{2\pi w}{b} \Big)}} \] Where w = Width of dislocation, and \(w = \frac{a}{1-\nu} \), a= inter-planer spacing
Important Points :
(1) For CPP \( a \uparrow \Rightarrow w \uparrow \Rightarrow \tau_{PN} \downarrow \Rightarrow \) Stress required for slip is less means ductile material.
(2) Slip will occure when \( \tau_{PN} \) is less , means slip will occure in Closed pack plane ( i.e., \( a \uparrow \) ) and closed pack direction \( b \downarrow \)
(3) In covalent crystal dislocation width(w) is very less => Difficult to move dislocation => brittle
(4) For ionic crystal, moderate value of \( \tau_{PN} \) is required. But brittle frature is observed due to large 'b'.

---

Resolved Shear Stress (\( \tau_{RSS} \))

\[ \tau_{RSS} = \frac{P}{A} = \frac{Fcos(\phi)}{\frac{A}{cos(\phi)}} \] \[ \Rightarrow \tau_{RSS} = \sigma cos(\lambda) cos(\phi) \] Special Cases :
(1) If \( \lambda = 90 \Rightarrow cos(\lambda) = 0\) => \( \tau_{RSS} = 0 \)
(2) If \( \phi = 90 \Rightarrow cos(\phi) = 0\) => \( \tau_{RSS} = 0 \)

Critical Resolved Shear Stress (\( \tau_{CRSS} \)) :
Slip in a material occures when the shearing stress on the slip plane in the slip direction reaches a threshold value called the critical resolved shear stress.

\[ \boxed{ \tau_{CRSS} = \sigma_{y} cos(\lambda) cos(\phi) } \]

Where \( cos(\lambda) cos(\phi) \) is called as Schmid Factor and \( \sigma_{y} =\) Yield Strength

Note :
(1) If we change the direction of stress w.r.t. slip plane and slip direction, \( cos(\lambda) cos(\phi) \) will also change but \( \tau_{CRSS} \) will not change. Hance \( \sigma_{y} \) will change => \( \sigma_{y} \) is anisotropy in nature.
(2) \( \tau_{CRSS} \) is a material property.
(3) Slip system with higher Schmid factor will be active slip system.

Condition For Dislocation Motion \[ \tau_{RSS} > \tau_{CRSS} \]